Artikel Inhoud
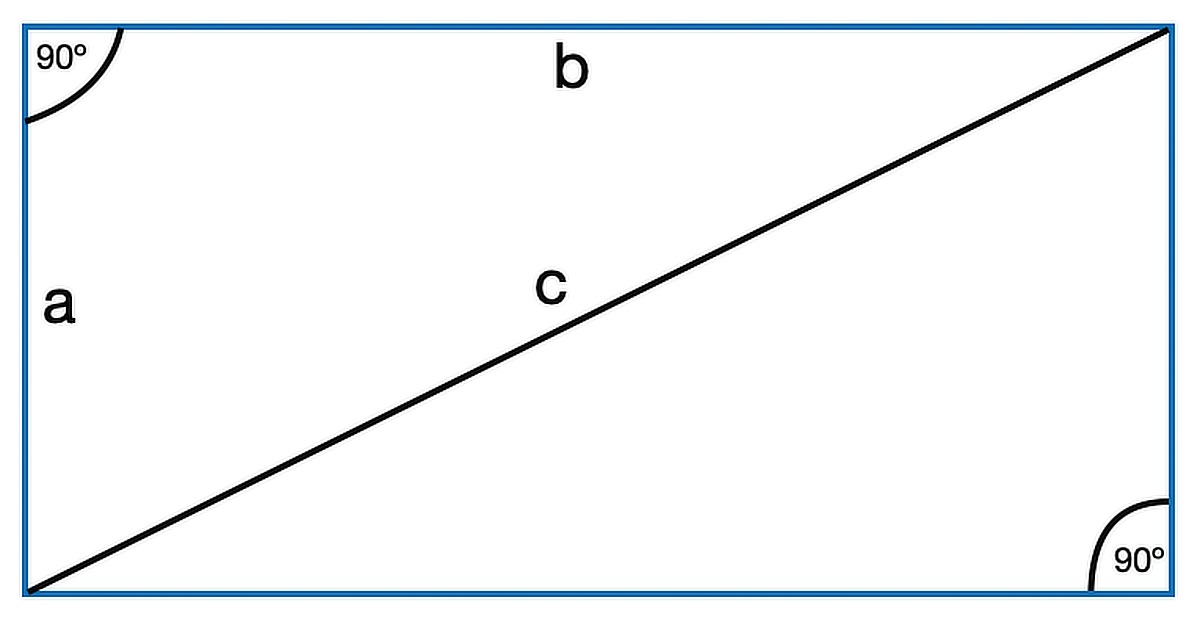
Wat zijn de muzikale mogelijkheden van een rechthoek? Vier zijden en vier gelijke hoeken impliceren symmetrie in vorm, maar ook deelbaarheid en gemeenschappelijkheid.
- 4/4 meter
- 4 secties
- 4 maten
- 4 herhalingen
- 4 + 4 = 8 Bar
- 8 + 8 = 16 repen
De hoeken zijn elk 90º. Door samengevatte variaties te creëren, krijgen we:
- 90
- 90 + 90 = 180
- 90 + 90 +90 = 270
- 90 + 90 + 90 + 90 = 360
Nadenken over hoeken en graden doet denken aan het concept van fase en fasegerelateerde effecten in audio, zoals fasemodulatie en fasevervormingssynthese.
Kwantiseren op een gelijkgestemde schaal:
- 90 Hz ligt het dichtst bij F#1
- 180 Hz ligt het dichtst bij F#2
- 270 Hz ligt het dichtst bij C#3
- 360 Hz is dicht bij F#3
Microtonaal denken:
- 90 Hz = F#2 minus 47 cent
- 180 Hz = F#3 minus 47 cent
- 270 Hz = C#4 minus 45 cent
- 360 Hz = F # 4 min 47 cent
- 47 Hz = F#0 plus 28 cent
- 45 Hz = F#0 minus 47 cent
- 28 Hz = A-1 plus 31 cent
- 31 Hz = B-1 plus 7 cent
- 7 Hz is onder het hoorbare, maar het is een bruikbare LFO-snelheid
Kanttekening: er zit 100 cent in elke 1/2 stap.
Denken in termen van harmonie:
Geselecteerde toonladders met deze noten zijn onder meer:
- F# eolische modus (natuurlijke mineur)
- F# Dorische modus
- F# Frygische modus
- F# harmonische mineur (+ alle bijbehorende modi)
- F# melodische mineur (+ alle bijbehorende modi)
- A majeur (+ alle bijbehorende modi)
- E majeur (+ alle bijbehorende modi)
- D majeur (+ alle bijbehorende modi)
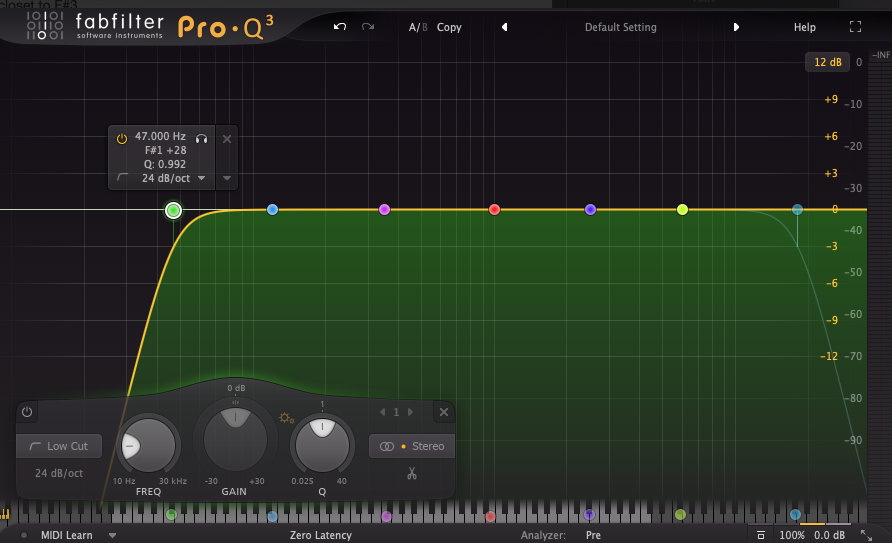
De hierboven genoemde frequenties kunnen worden gebruikt als parameterinstellingen in een filter of EQ:
- Afsnijfrequenties (LP, HP, BP, BR)
- Middenfrequenties (Bell, Notch)
- Helling of Q
De 4 zijden van een rechthoek doen denken aan een envelop met 4 fasen. Parallelle zijden zijn gelijk en er zijn 2 korte zijden en 2 lange zijden.
ADSR = aanval/verval/duurzaam/loslaten

Mogelijkheden:
- Aanvaltijd = vervaltijd
- Attack tijd = release tijd
- Release tijd = vervaltijd
- Sustain-niveau = 1/4 verzwakking in niveau na het vervalstadium = 0,75 op basis van een genormaliseerde amplitude (0 dB = 1,0)
Als we denken aan golflengten (met 1132 ft/seconde en 344 meter/seconde als geluidssnelheid) krijgen we:
- 90 Hz = 12,58 voet = 3,82 meter
- 180 Hz = 6,29 voet = 1,91 meter
- 270 Hz = 4,19 voet = 1,27 meter
- 360 Hz = 3,14 voet = 0,96 meter
Het is fascinerend dat de golflengte van 360 Hz met behulp van de geluidssnelheid van 1132 ft/seconde dicht bij pi = 3,14159265359 (in voet) komt.
Bovenstaande hoeveelheden kunnen worden gebruikt voor:
- LFO-tarieven
- Nagalmtijd (milliseconden of seconden)
- Vertragingstijd (milliseconden of seconden)
- Enveloptijden (milliseconden of seconden)
- Compressie parameter instellingen
- Instellingen voor ontstemming
Denk aan golfvormen – een rechthoekige golf is niets meer dan een vierkante golfvorm met een gewijzigde pulsbreedte-instelling.
Het voortdurend veranderen van de pulsbreedte wordt pulsbreedtemodulatie (PWM) genoemd en is een iconisch geluid in de synthese.
De rechthoekige golfvorm zou kunnen zijn:
- Een van de belangrijkste oscillatoren in een subtractieve synth
- Een draaggolf of modulerende oscillator in een FM-synth
- Een LFO-golfvorm die wordt gebruikt om elke parameter te moduleren
Om terug te komen op de “vier-heid” van de vorm, overweeg dan:
- De 4e voorinstelling
- 4 LFO’s
- 4 enveloppen
- 4 oscillatoren
- 4 instrumenten
- 4 lagen
- 4 delen
- 4 inzetstukken
- 4 verzendt
- 4 sporen
- 4 secties
- 4 geautomatiseerde parameters
- 4 noten akkoorden
- 4 ritmische divisies
- 4 Stapsequencers
- 4 octaven
- 4 Nootmelodie
- 4 akkoordprogressie
- 4-polig filter = 24 dB helling
- 4 verzen
- 4 koren
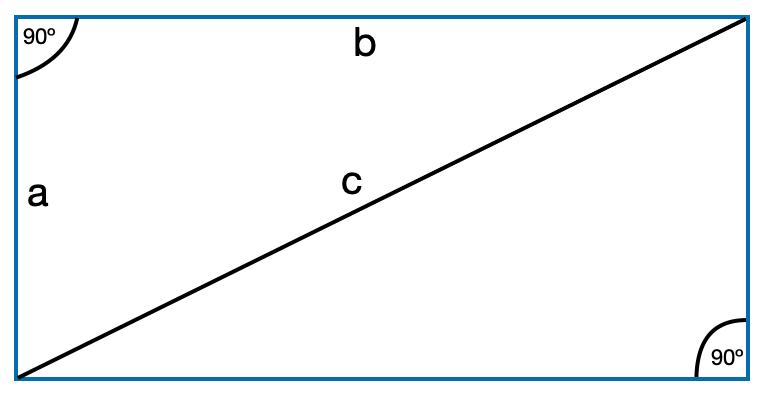
Een rechthoek in tweeën gedeeld vanuit tegenoverliggende hoeken resulteert in twee rechthoekige driehoeken en doet denken aan de stelling van Pythagoras (een2 + b2 = c2). Anders gezegd, de som van de gekwadrateerde waarden van de twee korte zijden is gelijk aan de gekwadrateerde waarde van de lange zijde of de hypotenusa. Denkend aan Pythagorus (ca. 570 – ca. 495 v. Chr.) doet denken aan de harmonische reeks en ook Pythagoras tuning systemen. Gebaseerd op een 12-toons Pythagoras-schaal gebouwd op een F#-grondtoon, krijgen we de volgende ontstemmingsopstelling van Logic Pro’s alternatieve afstemmingsparameters.
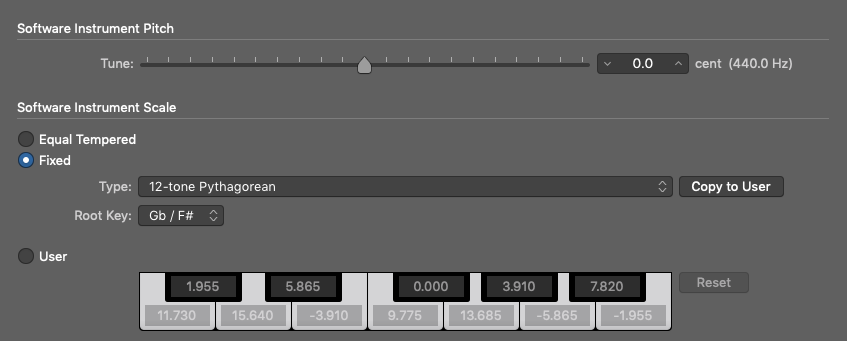
Ook uit de bovenstaande paragraaf kunnen we aanvullende opmerkingen abstraheren:
- C-noot (van a2 + b2 = c2)
- 570 Hz = C#4 plus 48 cent (geboorte van Pythagorus)
- 495 Hz = B3 plus 4 cent (dood van Pythagorus)
Een rechthoek bestaat uit 4 aaneengesloten lijnen. Als we op één punt beginnen en de lijn volgen, keer je terug naar het begin – een soort samenvatting:
- 4 melodische lijnen
- 2 lange rijen
- 2 korte lijnen
Nadenken over harmonisch ritme:
- 4 akkoordenpatroon
- 2 akkoordenpatroon
- 2 tellen per akkoord
- 4 tellen per akkoord
Terugkerend naar de waarde van 90º, overweeg dan:
- 90 bar
- 90 seconden
- 90 slagen
- 180 repen
- 180 seconden
- 180 slagen
- enz.
Dus wat is het punt?
Tegen die tijd (als je zover bent gekomen), denk je misschien: wat heeft het voor zin? Het punt is dat er geen punt hoeft te zijn. Muziek hoeft niet te gaan over het uiten van emoties of gevoelens, tenzij je dat wilt. Het hoeft niet de regels van de westerse harmonie te volgen om ‘goed’ te klinken. En het hoeft absoluut niet “juist” te zijn op een meetbare manier.
De regels van contrapunt en stemvoering zijn ontwikkeld door componisten en theoretici die ernaar streefden een bepaalde esthetiek te behouden en te codificeren. Mensen zoals Heinrich Schenker (1868-1935) theoretiseerde dat er een onderliggende structuur was die niet alleen kon worden gebruikt om de samenhang van een muziekwerk te verklaren, maar dat regels konden worden geëxtrapoleerd en gebruikt als een soort structureel sjabloon om nieuw werk te creëren dat even coherent en “succesvol.”
Velen zouden beweren dat deze aanpak prima werkt. Het lijdt geen twijfel dat de gladheid bereikt door het gebruik van veelgebruikte stemleidende constructies, zoals het vermijden van parallelle 5ths en octaven, zijn ons bekend in de oren geworden en kunnen in allerlei genres worden gevonden. Terwijl Arnold Schönberg (een van de ontwikkelaars van dodecafonische of 12-toonsharmonie) ernaar streefde de romantische toonverhoudingen van de 19e eeuw uit te breiden naar een atonale esthetiek, liet hij niet alle regels die tot dan toe waren vastgesteld volledig los.
John Cage, de hedendaagse Amerikaanse componist die bekend staat om zijn geprepareerde pianostukken, het zogenaamde ‘stilte’-stuk 4’33” en het gebruik van onbepaaldheid bij het maken van muziek, vertelt een verhaal toen hij een leerling van Schönberg was. Zoals ik in een vorig artikel al aangaf:
“Als jonge componist [Cage] studeerde contrapunt bij Arnold Schönberg, die zijn studenten vaak vroeg om elke mogelijke stemleidende oplossing voor een bepaalde melodie te bieden. Hij zou dan vragen: “Wat is het principe dat ten grondslag ligt aan alle oplossingen?” Pas jaren later realiseerde Cage zich dat wat alle oplossingen gemeen hadden, de vraag was!”
Die relevantie van de vraag is cruciaal, aangezien elk kunstwerk niet met één, maar met een reeks vragen begint. In termen van nieuw muziekstuk kun je je afvragen:
- Wat wordt de instrumentatie?
- Wat zullen de onderliggende harmonische relaties zijn?
- Wat zal de ritmische inhoud zijn?
- Wat zal het tempo zijn?
- enz.
Als de antwoorden op de vragen elke keer hetzelfde zijn, kun je zien hoe redundantie uiteindelijk een probleem kan worden. Evenzo, als dezelfde vragen zelf keer op keer worden gesteld, kunnen uw keuzes een gewoonte en routine worden.
Ik gebruikte het proces van het abstraheren van muzikale constructies uit een rechthoek om te suggereren dat muzikale ideeën overal om ons heen zijn. Niet alleen in termen van directe geluidsbronnen zoals veldopnames en gevonden geluiden, maar in termen van numerologie, visuele en geometrische evenredigheid, wiskunde, natuurkunde, filosofie – letterlijk overal.
De onderliggende constructies van een muziekwerk zijn echter veel minder belangrijk dan het eindresultaat. Het hardnekkig gebruiken van een vooraf bedachte methodiek om je keuzes te dicteren tijdens het componeren zonder je oor en intuïtie te laten ingrijpen of de keuzes die uit het systeem naar voren komen aan te passen, zou niets meer zijn dan een oefening in koppige rationaliteit, los van de creatieve impuls. Om een cliché te gebruiken: regels zijn er om overtreden te worden. Dit geldt vooral voor de regels die je zelf bedenkt.
Het maakt de gemiddelde luisteraar niet uit welke schaal je gebruikt of wat de snelheid van een LFO is. En het kan hen niets schelen als je een of ander waardeloos nummer op een rechthoek baseert. Maar als het hen emotioneel raakt of intellectueel of beide betrekt, heb je een ‘succesvol stuk’. Voor componisten en producers is de aanzet om te schrijven en de motivatie om gewoon te beginnen soms ongrijpbaar. Als je zoveel muzikale ideeën uit een simpele rechthoek kunt halen, moet er een schat aan ideeën zijn op de plek waar je dit artikel leest.
Bekijk mijn andere artikelen, recensies, interviews, en mijn video-tutorialreeks, Synthese 101 exclusief beschikbaar op The Pro Audio Files.
Volg me op Twitter: @PMantione
Instagram: philipmantione
CreditSource link





